Radioaktivitet

Logaritmefunktionerne er interessante i forhold til radioaktivitet, da radioaktivt stof henfalder som en eksponentielt aftagende funktion af tiden.

At det er en eksponentielt aftagende funktion gør, at vi kan lave følgende funktion: m(t) = m₀ ∙ a^t. I denne funktion står bogstaverne for følgende:

     m₀ er vores begyndelsesværdi og betegner det antal gram, vi har af det radioaktive stof.

     t står for tidspunktet.

     m(t) fortæller hvor meget endnu ikke-omdannet radioaktivt stof i gram, der er tilbage.

     Grundtallet a skal være større end 0, men mindre end 1, da funktionen er aftagende.

Da vi gerne vil have Eulers tal e til at stå som fremskrivningsfaktor, laver vi nogle omregninger, fordi vi ved, at a = e^ln(a). Derfor byttes a ud med dette udsagn.

m(t) = m₀ ∙ a^t <=> m(t) = m₀ ∙ (e^ln(a))^t <=> m(t) = m₀ ∙ e^-kt

     Her er -ln(a) blevet udskiftet med k, der kaldes henfaldskonstanten.

Vha. halveringstiden og nogle omregninger kan vi finde både femskrivningsfaktoren og henfaldskonstanten. I dette tilfælde vælger vi at kigge på en Radium-ion, der har en halveringstid på 1620 år.

Vi starter med at finde fremskrivningsfaktoren a vha. halveringstiden.

a = (1/2)^(1/T) <=> a = (1/2)^(1/1620) <=> a = 0,9995722

Med fremskrivningsfaktoren er det også muligt at regne sig frem til henfaldskonstanten, da vi jo tidligere indførte, at k = -ln(a).

k = -ln(a) <=> k = -ln(0,9995722) <=> k = 0,0004279

Dermed kan man altså skrive formlen på disse to forskellige måder:

     m(t) = m₀ ∙ a^t => m(t) = m₀ ∙ 0,9995722^t

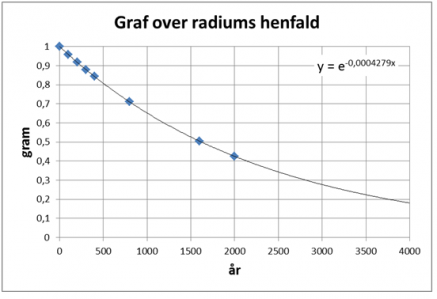
     m(t) = m₀ ∙ e^-kt => m(t) = m₀ ∙ e^-0,0004279*t

I begge formler er m₀ stadig vores begyndelsesværdi. For at få det illustreret, vil vi regne lidt mere på det hele. Vi sætter begyndelsesværdien til at være 1 g og får følgende skema og illustration: