Den naturlige logaritmefunktion

Den naturlige logaritmefunktion er den logaritmefunktion, der har grundtallet e. Dette betyder, at denne logaritmefunktion er den omvendte funktion til f(x) = e^X. Dermed har vi altså, at e^lnx = x og ln(e^x) = x.

Definitionsmængden for den naturlige logaritme er Dm(ln) = ]0;∞[, mens værdimængden er Vm(ln) = R.

Den eksponent som e skal opløftes i for at give et tal, er den værdi, man får, når man tager den naturlige logaritme til det samme tal. Et eksempel herpå er: ln(22.026,5) ≈ ln(e¹⁰) = 10

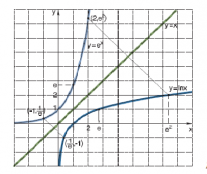
Her er graferne tegnet for funktionerne f(x) = e^X og g(x) = ln(x). Disse to var jo som tidligere skrevet hinandens omvendte funktioner, hvorved deres grafer vil ligge symmetrisk omkring linjen y = x. De er altså hinandens spejlbilleder, som vi også kan se på grafen.

Grundtallet for den naturlige logaritmefunktion findes som det tal, hvis funktionsværdi på y-aksen er 1. Dvs. lne = 1